Why you need Checklist ?
Learn Exact Topic for the Exam
Check your Progress in your preparation
Acts as a GUIDE in your preparation



























Linear Algebra
S.No Topic Tick
1 Given Linear Transformation, Find a) Rank, b) Nullity c) Range Space d) Null Space
2 Given Matrix Form of Linear Transformation, Find a) Rank, b) Nullity c) Range Space d) Null Space
3 Given Linear Transformation with Two Different Bases Sets, Find Matrix
4 Given Linear Transformation with Standard Basis. Find Matrix relative to New Basis Set
5 State and Prove Cayley Hamilton theorem
6 Given Homogeneous Equation, Find Dimension and Basis
7 Find Rank of Matrices
8 Given Matrix, Find Inverse and Express High order Matrix Polynomial in terms of A
9 Given Matrices, find Eigen Values and eigen Vectors
10 Given Matrix A, Find A(power of 300 ) using Cayley Hamilton
11 Find Inverse using ONLY ELEMENTART ROW OPERATION
12 Given Linear Eqn , Find Condition fora) No Solutionb) Unique Solutionc) Infinite Solutions
13 Given Matrix A , Find NonSingular Matrix P , such that P(inverse)*A*P is a diagonal matrix
14 Given Hermitian Matrix A , Find NonSingular Matrix P , such that P(transpose)*A*P is a diagonal matrix
15 Given Vector Set: Check for Linear Independency (In Real Field and Complex Field)
16 Prove DIM (A + B) = DIM A + DIM B……
17 Problems using DIM( A +B) relation
18 State and Prove Rank Nullity Theorem
19 Reduction to Quadratic Form, Find Index, Signature, Rank
20 Reduce the quadratic form 7x2+6y2+5z2-4xy-4yz to the canonical form
21 Problems on Unitary, Hermitian given in Krishna Series-Matrices
22 Show A.(adj A) = |A|* I Show adj (adj A) = A { power of (n-2) square }
23 Theorems1) Similar Matrix have same Eigen Values2) Distinct NonZero Eigen Vectors are Linear Independent3) Eigen values of A (Adj A) is Real and show Trace (A Adj A) = Trace (Adj A * A)5) Characteristic Root of Adj A
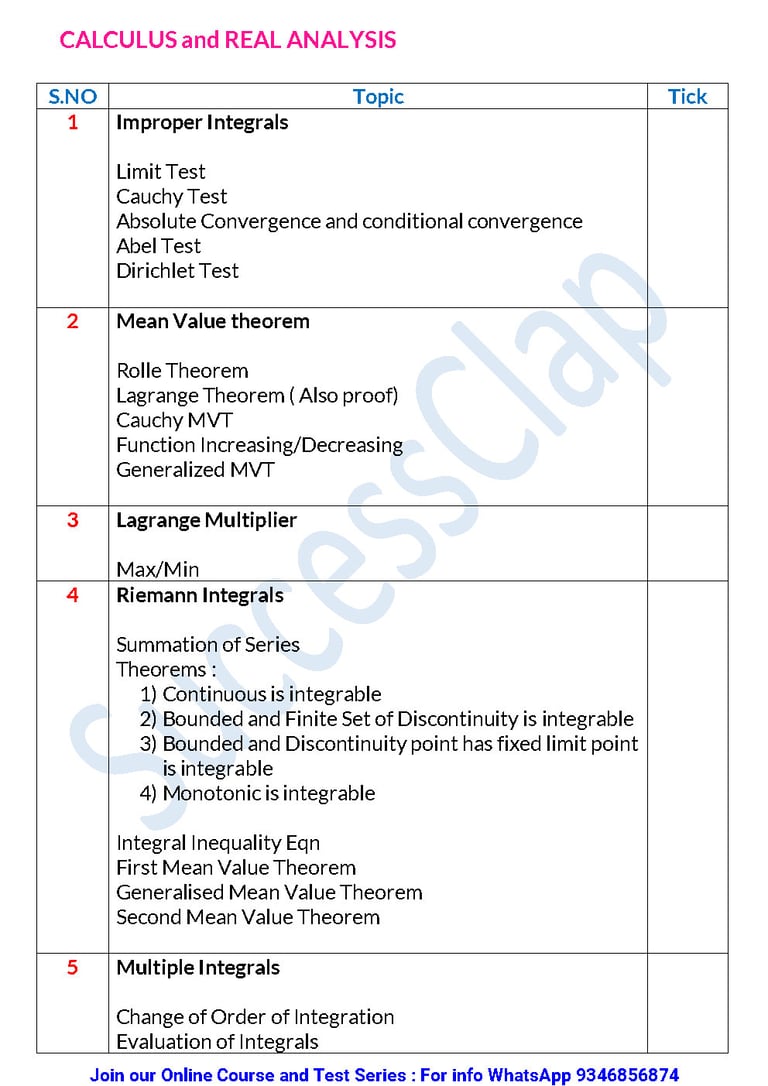
CALCULUS and REAL ANALYSIS
S.NO Topic Tick
1 Improper Integrals Limit TestCauchy TestAbsolute Convergence and conditional convergenceAbel TestDirichlet Test
2 Mean Value theorem Rolle TheoremLagrange Theorem ( Also proof)Cauchy MVTFunction Increasing/DecreasingGeneralized MVT
3 Lagrange Multiplier Max/Min
4 Riemann Integrals Summation of SeriesTheorems :1) Continuous is integrable2) Bounded and Finite Set of Discontinuity is integrable3) Bounded and Discontinuity point has fixed limit point is integrable4) Monotonic is integrable Integral Inequality EqnFirst Mean Value TheoremGeneralised Mean Value TheoremSecond Mean Value Theorem
5 Multiple Integrals Change of Order of IntegrationEvaluation of Integrals
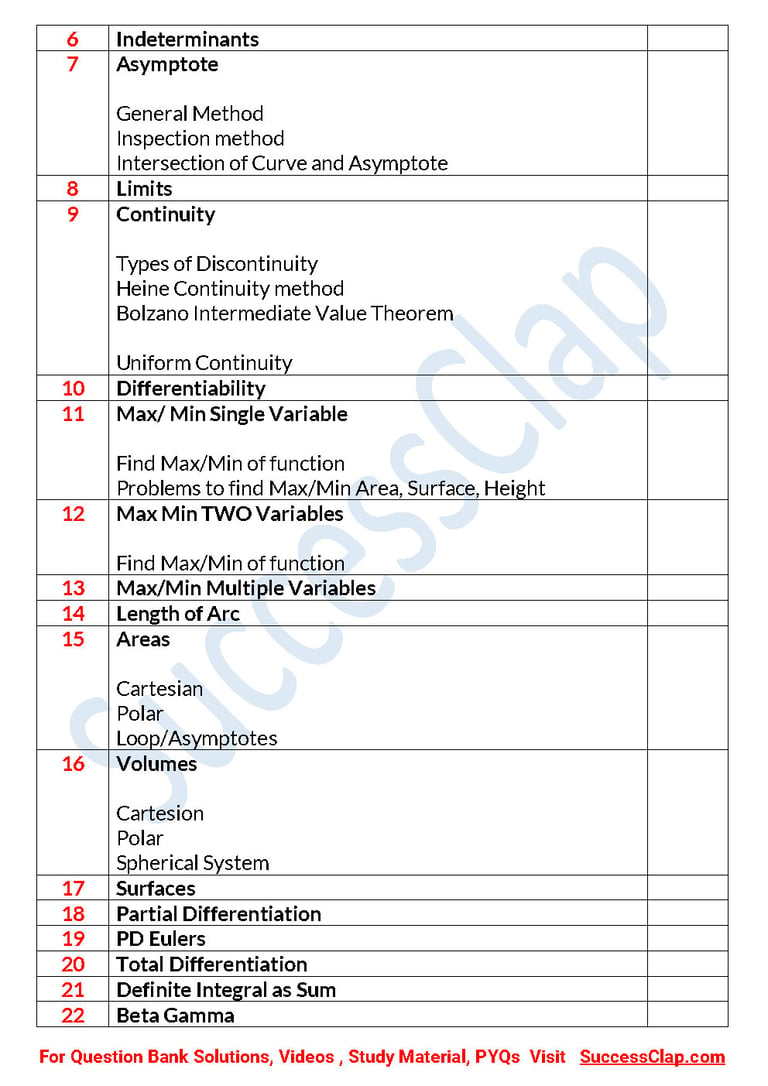
6 Indeterminants
7 Asymptote General MethodInspection methodIntersection of Curve and Asymptote
8 Limits
9 Continuity Types of DiscontinuityHeine Continuity methodBolzano Intermediate Value Theorem Uniform Continuity
10 Differentiability
11 Max/ Min Single Variable Find Max/Min of functionProblems to find Max/Min Area, Surface, Height
12 Max Min TWO Variables Find Max/Min of function
13 Max/Min Multiple Variables
14 Length of Arc
15 Areas CartesianPolarLoop/Asymptotes
16 Volumes CartesionPolarSpherical System
17 Surfaces
18 Partial Differentiation
19 PD Eulers
20 Total Differentiation
21 Definite Integral as Sum
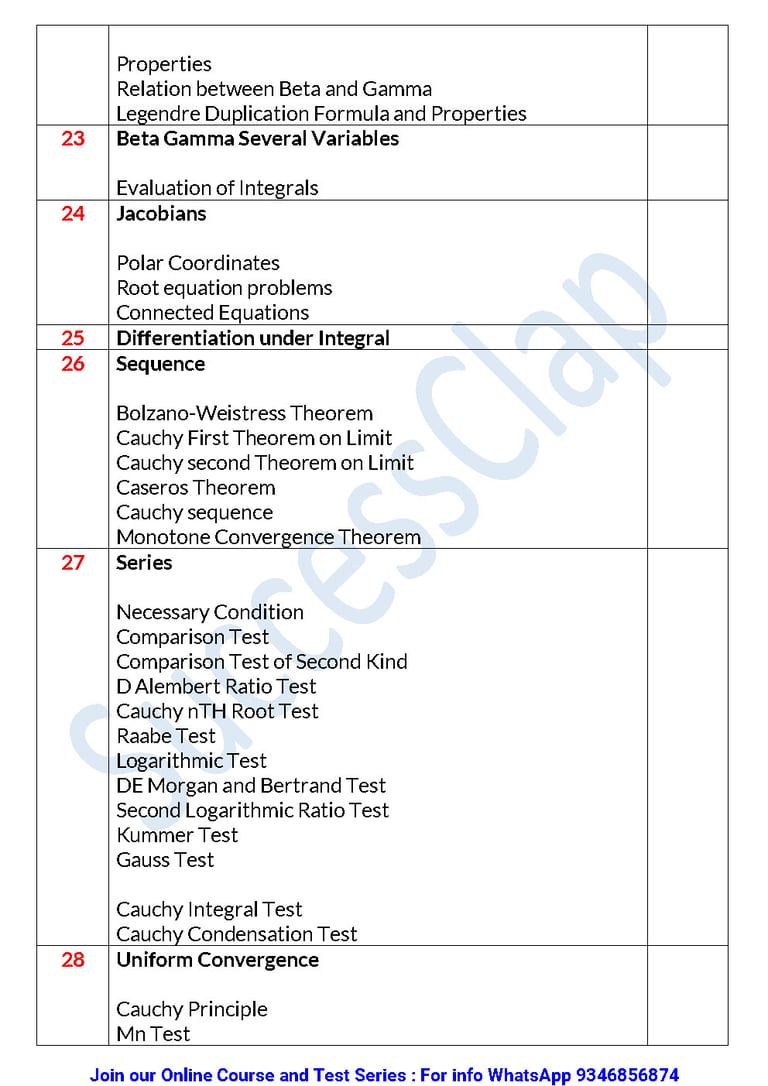
22 Beta Gamma PropertiesRelation between Beta and GammaLegendre Duplication Formula and Properties
23 Beta Gamma Several Variables Evaluation of Integrals
24 Jacobians Polar CoordinatesRoot equation problemsConnected Equations
25 Differentiation under Integral
26 Sequence Bolzano-Weistress TheoremCauchy First Theorem on LimitCauchy second Theorem on LimitCaseros TheoremCauchy sequenceMonotone Convergence Theorem
27 Series Necessary ConditionComparison TestComparison Test of Second KindD Alembert Ratio TestCauchy nTH Root TestRaabe TestLogarithmic TestDE Morgan and Bertrand TestSecond Logarithmic Ratio TestKummer TestGauss Test Cauchy Integral TestCauchy Condensation Test
28 Uniform Convergence Cauchy PrincipleMn TestWeirstrass TestAbel TestDirichlet Test Properties ona)Sumb) Differntiabilityc) Integrability
29 Functions of Several Variables LimitContinuityDifferentiability
30 MVT Taylor Maclurin Expansion
NUMERICAL ANALYSIS
S.No Topic Tick
1 Obtain (a)Quadrature Formula, (b)Trapezoid Rule, (c)Simpson 1/3, (d) Simpson3/8. Rule and also (e)derive their Error Formula for ALL RULES.
2 Derive Newton Raphson Method,b) Find Condition for its convergencec) Show rate of convergence is quadraticd) Explain its merits and demerits.
3 Bisection Method
4 Regula Falsi Method
5 Secant Method
6 Iteration Method and its Convergence
7 Derive Newton Gregory Forward interpolation formula, and its Error.
8 Derive Newton Gregory’s Backward Interpolation formula and its Error
9 Derive Lagrange interpolation formula and derive its Error formula
10 Prove that Lagrange’s formula can be put in the form of .
11 Show that the sum of Lagrangian coefficient is unity.
12 Use Lagrange’s interpolation formula to express the function a) b) as sums of partial fractions.
13 Find the parabola passing through points (0,1) (1,3) and (3,55) using Lagrange’s formula.
14 Derive Gauss Quadrature Formula.
15 Evaluate the integral using Gauss Quadrature n=5.Find the value of the integral using Gauss Quadrature n=4.
16 Solve ODE Problems a) Euler b) Euler Modified c)Runge Kutta Order 1, Order 4
17 Solve Linear Eqns a) Gauss Elimination b) Gauss Jordan c) Gauss Seidel d) Gauss Jacobi
18 Use Gauss Jordan to Find Inverse
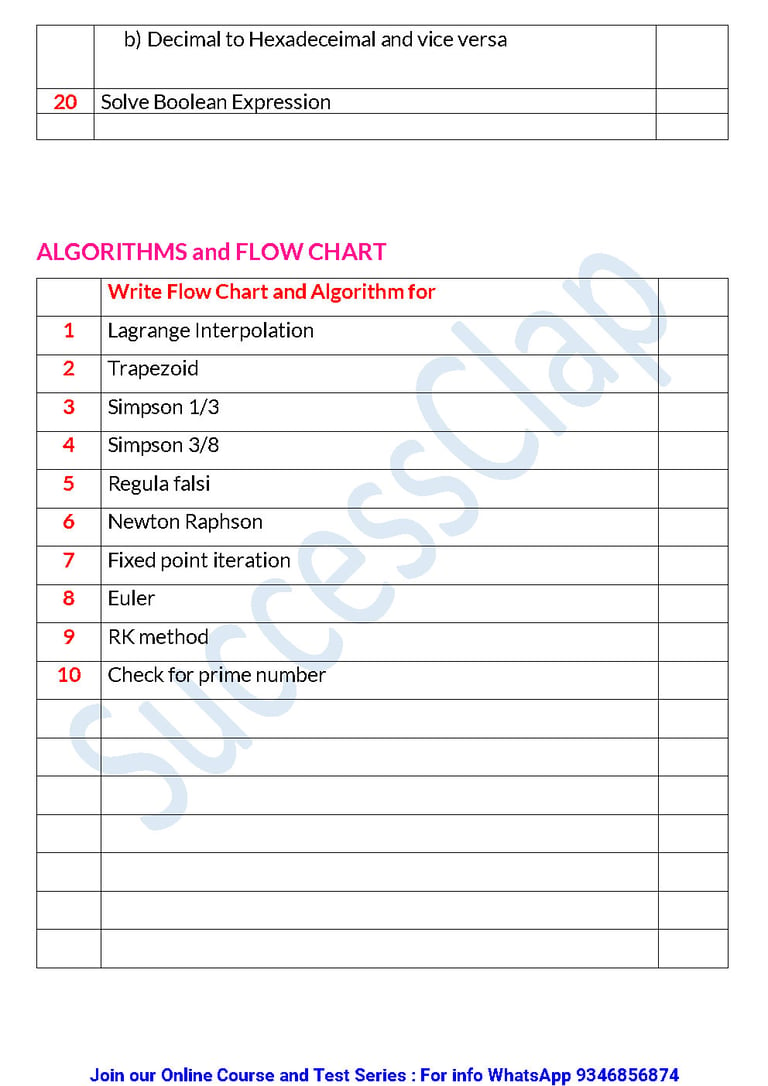
19 Conversion a) Decimal to Octogonal and Vice versab) Decimal to Hexadeceimal and vice versa
20 Solve Boolean Expression
ALGORITHMS and FLOW CHART
Write Flow Chart and Algorithm for
1 Lagrange Interpolation
2 Trapezoid
3 Simpson 1/3
4 Simpson 3/8
5 Regula falsi
6 Newton Raphson
7 Fixed point iteration
8 Euler
9 RK method
10 Check for prime number
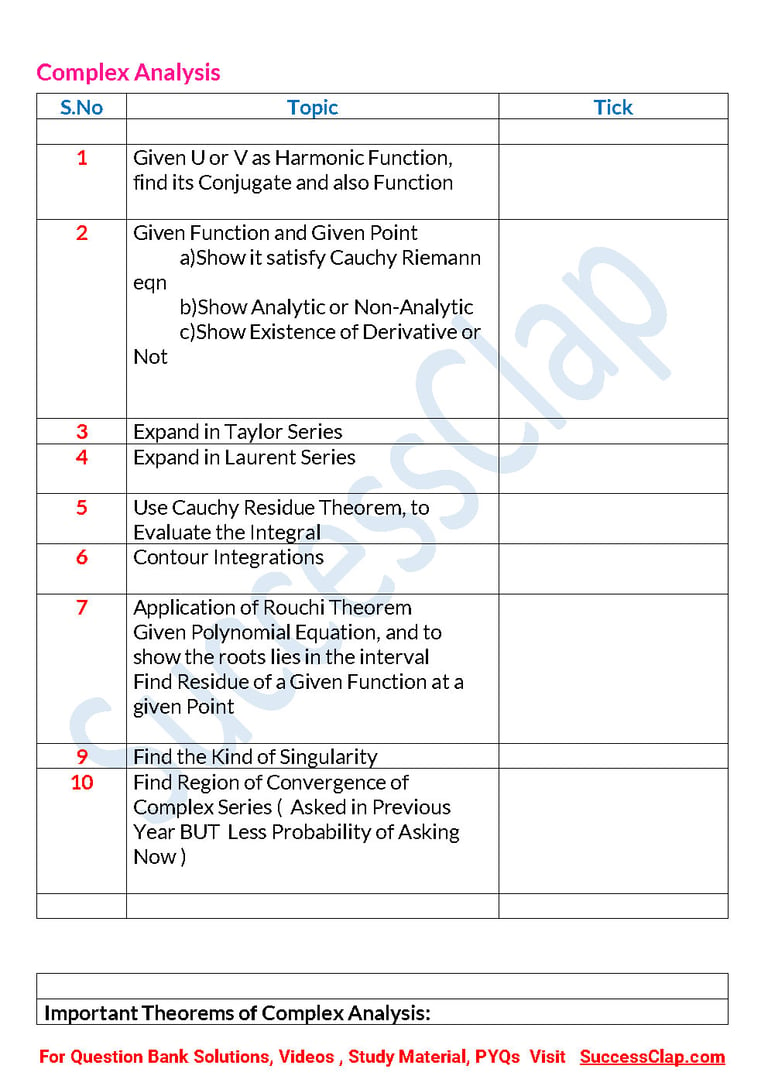
Complex Analysis
S.No Topic Tick
1 Given U or V as Harmonic Function, find its Conjugate and also Function
2 Given Function and Given Pointa)Show it satisfy Cauchy Riemann eqnb)Show Analytic or Non-Analytic c)Show Existence of Derivative or Not
3 Expand in Taylor Series
4 Expand in Laurent Series
5 Use Cauchy Residue Theorem, to Evaluate the Integral
6 Contour Integrations
7 Application of Rouchi TheoremGiven Polynomial Equation, and to show the roots lies in the intervalFind Residue of a Given Function at a given Point
9 Find the Kind of Singularity
10 Find Region of Convergence of Complex Series ( Asked in Previous Year BUT Less Probability of Asking Now )
Important Theorems of Complex Analysis: a) Prove that every power series representing an analytic function inside its circle of convergence b) (Fundamental theorem of Algebra)Let P(z) = a0 + a1z + ….+anzn, where n > 1 and an 0 so that P(z) is a polynomial of degree one or greater. Then the equation P(z) =0 has at least one root. f) Every polynomial equation P(z) = a0+a1z+a2z2+…anzn = 0, where n > 1, an . g) If f(z) has a pole of order m at z0, then the function φ defined by φ(z) = (z-z0)m f(z) has a removable singularity at z0 and φ(z0) Also show that the residue at z0 is given by . h) Show that a function which has no singularity in the finite part of the plane and has a pole of order n at infinity is a polynomial of degree n. (i) A polynomial of degree n has no singularities in the finite part of the plane but has a pole of order n at infinity. (j) If a function f(z) is analytic for all finite values of z and as ∣z∣ k then f(z) is a polynomial of degree < k. (k) If f(z) is a function such that for some positive integer m, a value φ(z0) exists with φ(z0) 0 such that the function φ(z) = (z-z0)m f(z) is analytic at z0. Then f(z) has a pole of order m at z0.
Linear Programming
S.No Topic Tick
1 Formulation of LPP
2 Graphical Method of Solution
3 Simplex Method
4 Big M Method
5 Construct Dual and Solve
6 Transportation Problem
7 Assignment Problem
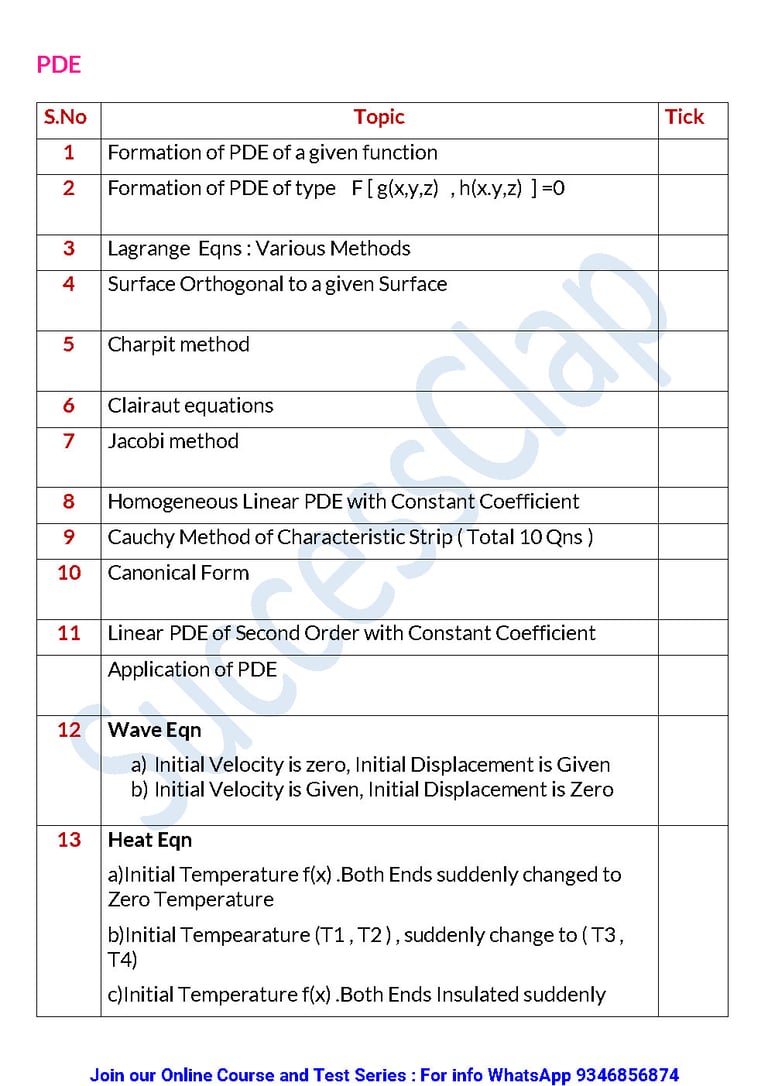
PDE
S.No Topic Tick
1 Formation of PDE of a given function
2 Formation of PDE of type F [ g(x,y,z) , h(x.y,z) ] =0
3 Lagrange Eqns : Various Methods
4 Surface Orthogonal to a given Surface
5 Charpit method
6 Clairaut equations
7 Jacobi method
8 Homogeneous Linear PDE with Constant Coefficient
9 Cauchy Method of Characteristic Strip ( Total 10 Qns )
10 Canonical Form
11 Linear PDE of Second Order with Constant Coefficient
Application of PDE
12 Wave Eqna) Initial Velocity is zero, Initial Displacement is Givenb) Initial Velocity is Given, Initial Displacement is Zero
13 Heat Eqna)Initial Temperature f(x) .Both Ends suddenly changed to Zero Temperatureb)Initial Tempearature (T1 , T2 ) , suddenly change to ( T3 , T4)c)Initial Temperature f(x) .Both Ends Insulated suddenlyd)At t=0 distribution is f(x). Suddenly One end is kept at T1 and other end Insullated
14 Laplace Eqnsa)Three sides Temerature is 0, Other side f(x)b)Two sides Temperature is 0, One side f(x), Other side at Infinte Longc)One side Insulated ( X-Axis)d)One Side Insulated ( Opposite side of X-Axis)e)Two sides Insulated , X-axis side f(x), Other side 0f)Two sides Insulated, X-axis side 0, Other side f(x)g)Three sides Insulated
15 Laplace in Polar Coordinate Sysytema)SemiCircular Plateb)Circular Arcc)Circular Plated)Circular Annulus
MECHANICS
S.No Topic Tick
1 Moment of Inertia
2 D Alembert Principle Problems
3 Lagrange Eqns
4 Hamilton Eqns
5 Fixed Axis Motions
6 Motion in 2Dimension
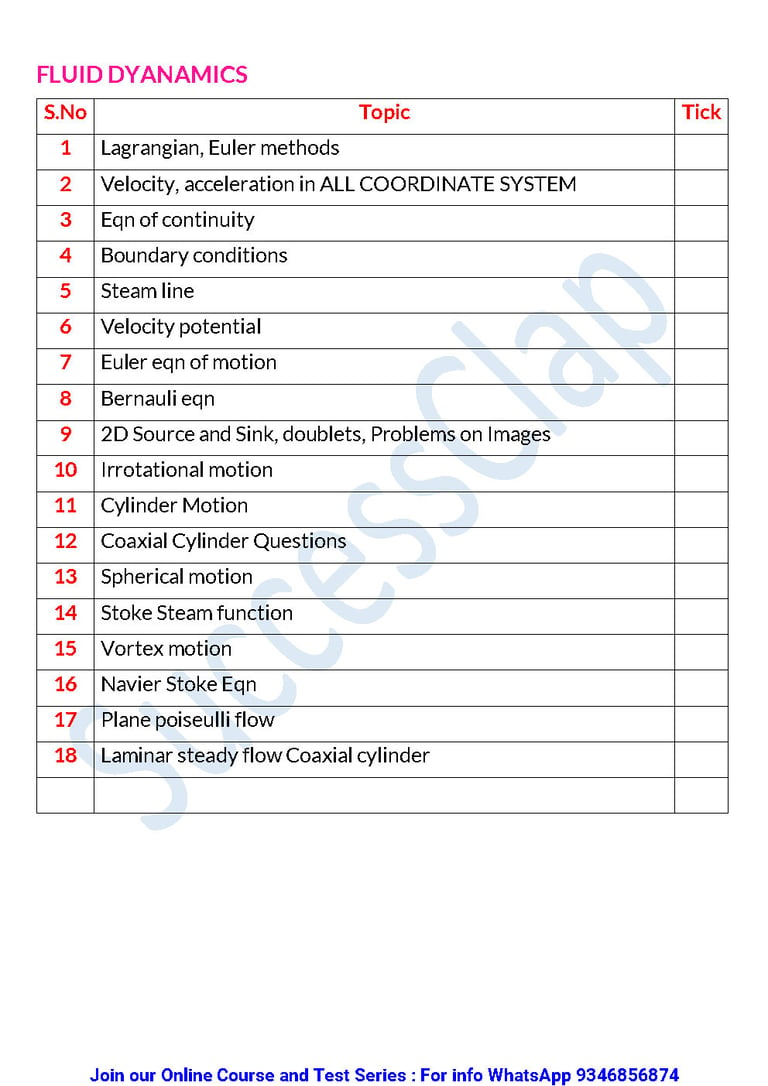
FLUID DYNAMICS
S.No Topic Tick
1 Lagrangian, Euler methods
2 Velocity, acceleration in ALL COORDINATE SYSTEM
3 Eqn of continuity
4 Boundary conditions
5 Steam line
6 Velocity potential
7 Euler eqn of motion
8 Bernauli eqn
9 2D Source and Sink, doublets, Problems on Images
10 Irrotational motion
11 Cylinder Motion
12 Coaxial Cylinder Questions
13 Spherical motion
14 Stoke Steam function
15 Vortex motion
16 Navier Stoke Eqn
17 Plane poiseulli flow
18 Laminar steady flow Coaxial cylinder
Analytic Geometry
S.No Topic Tick
Straight Lines
1 Find coordinate the foot of perpendicular from given point to a plane. And also find distance
2 Plane and St line: Parallel/ Perpendicular / Coincide
3 Projection of Line on Plane
4 Condition for Coplanar Lines
5 Determine Eqn of St Line intersecting two given Lines
6 Find Perpendicular distance of a point from line and its foot coordinate
7 Intersection of 3 Planes
Shortest Distance
1 Find SD between two lines and obtain eqn of SD (Very Imp)Projection MethodTwo Lines in Symmetric FormOne-line General, Other Symmetric FormTwo lines in General Form
1 Skew LinesFind locus of line, which intersects set of lines or function
Planes
1 Eqn of plan through 3 points
2 Angle between planes
3 Variable Plane Problems
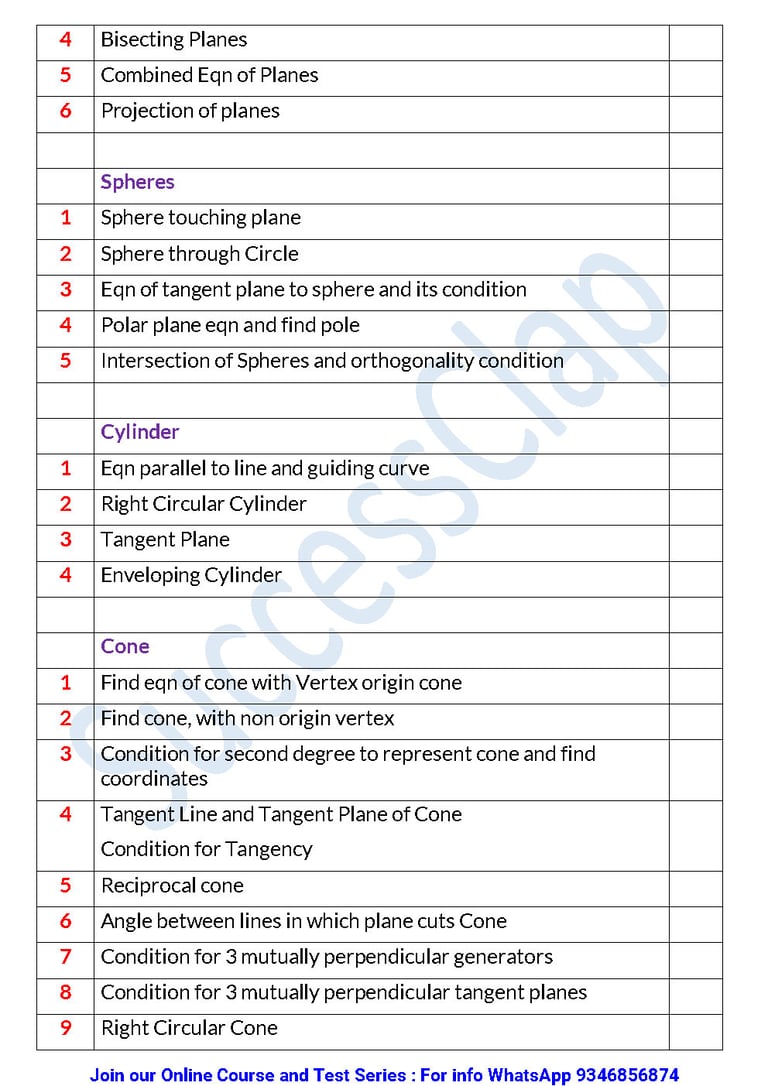
4 Bisecting Planes
5 Combined Eqn of Planes
6 Projection of planes
Spheres
1 Sphere touching plane
2 Sphere through Circle
3 Eqn of tangent plane to sphere and its condition
4 Polar plane eqn and find pole
5 Intersection of Spheres and orthogonality condition
Cylinder
1 Eqn parallel to line and guiding curve
2 Right Circular Cylinder
3 Tangent Plane
4 Enveloping Cylinder
Cone
1 Find eqn of cone with Vertex origin cone
2 Find cone, with non origin vertex
3 Condition for second degree to represent cone and find coordinates
4 Tangent Line and Tangent Plane of ConeCondition for Tangency
5 Reciprocal cone
6 Angle between lines in which plane cuts Cone
7 Condition for 3 mutually perpendicular generators
8 Condition for 3 mutually perpendicular tangent planes
9 Right Circular Cone
10 Enveloping Cone
Central Conicoids
1 Find Eqn of Tangent planeCondition for Tangency
2 Director Sphere
3 Polar Planes, Pole
4 Locus of Chord Bisected at a given point
5 Normal to Conicoids
6 Prove 6 normals to ellipsoid
7 Find cubic curve through feet of normal
8 Diametral Plane
9 Problems on Semi conjugate diameter properties
STATICS and DYNAMICS
S.No Topic Tick
1 Rectilinear Motion
2 SHM
3 Constrained Motion
4 Projectile Motion
5 Problems on Central Forces
6 Motion in a Plane
7 Work, Energy,Impulse
8 Stable and Unstable Equilibrium
9 Common Catenary
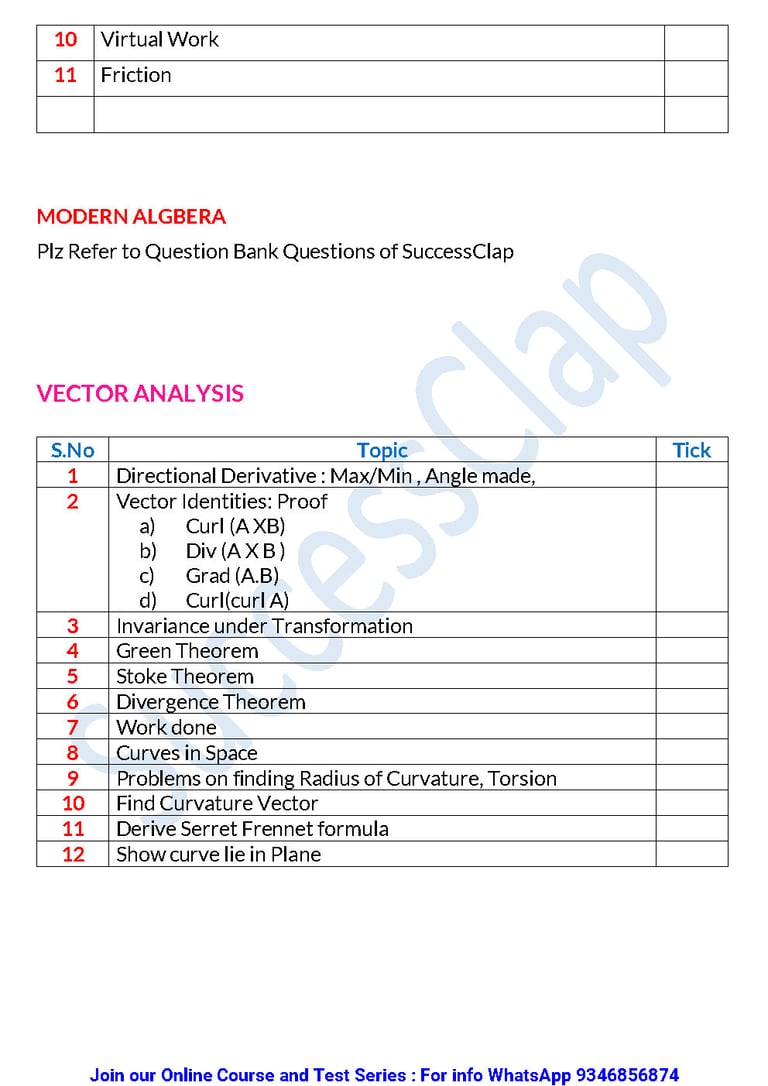
10 Virtual Work
11 Friction
MODERN ALGBERAPlz Refer to Question Bank Questions of SuccessClap
VECTOR ANALYSIS
S.No Topic Tick
1 Directional Derivative : Max/Min , Angle made,
2 Vector Identities: Proofa) Curl (A XB)b) Div (A X B )c) Grad (A.B)d) Curl(curl A)
3 Invariance under Transformation
4 Green Theorem
5 Stoke Theorem
6 Divergence Theorem
7 Work done
8 Curves in Space
9 Problems on finding Radius of Curvature, Torsion
10 Find Curvature Vector
11 Derive Serret Frennet formula
12 Show curve lie in Plane
ODE
S.No Topic Tick
1 Formation of DE
2 Eqn of 1st Order, 1st DegreeLinear Differential EqnsEqn reducible to Linear formBernauli Eqn
3 List of Important Results like Subnornal,subtangent, length of normal and tangent, Eqn of Tangent and NormalTangent and Normal X and Y interceptPolar subtangent, subnormal, length of tangent, normal
4 Orthogonal Tarajectory/Oblique Trajectory Eqn
5 Eqn of First Order but not of first degreeSolvable for pSolvable for xSolvable for yLagrange formEqn in Claurait FormEqn reducible to Caurait formSingular Soln
6 Linear Differential Eqns with Consatnt Coefficients
7 Homogeneous Linear Eqn/Cauchy Euler EqnLegendre linear eqns
8 Method of variation of parameters
9 Linear Eqn of Second OrderReduction with One known integralReduction to NormalChanging independent variable
10 Laplace
11 Inverse Laplace
12 Application to initial value problems for 2nd order linear equations with constant coefficients.


